Adaptive filters for signal processing: a comparative study

1. Introduction

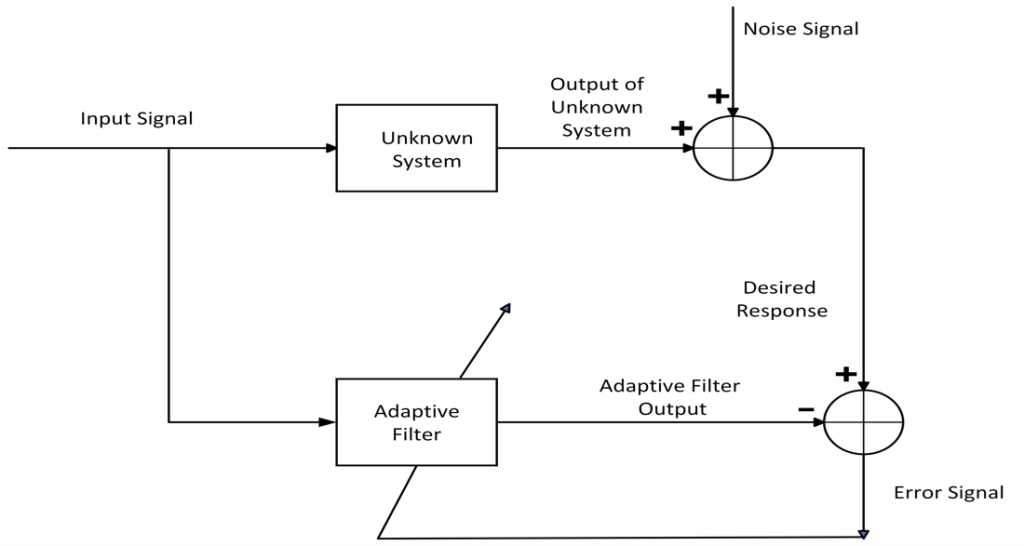
In some applications, the system or environment where processing is happening is unknown or time-dependant. In such applications, adaptive filters are required because they possess self-adjusting capabilities. An adaptive filter is mainly a digital filter that will adjust its filter parameters (coefficients) to converge the filter to the optimal solution of defined cost function using input data from the environment. The main target of these filters is to estimate the unknown entity of an input signal. They are used to reshape certain input signals in such a way that the filter output is a good estimate of the given desired signal.

The two steps involved in adaptive filtering process are: –

1. Filtering process,which produces an output signal in response to the given input signal using the updated filter coefficients, which later helps to adjust filter parameters in the adaptation process.
2. Adaptation process,to adjust the filter parameters according to the time varying environment. In this step, filter parameters (coefficients) are updated so that the cost function converges to its optimal solution by finding the best match between the desired signal and filter output.

The major applications of adaptive filters include noise cancellation, acoustic echo cancellation, bio-medical signal enhancement, equalizations of communication channels, active noise control, system identification, speech coding, multi-channel noise reduction and adaptive control systems. It works generally for the adaptation of signal-changing environments, and unknown or time-varying noise. For example: in echo cancellation, a dynamic mathematical model of channel that creates echo is generated by continuously monitoring the received signal. This model is used to create an estimate of echo path which is then subtracted from the signal to remove the effect of echo from desired signal.

2. Adaptive filter algorithms

Different kinds of adaptive filter algorithms includes

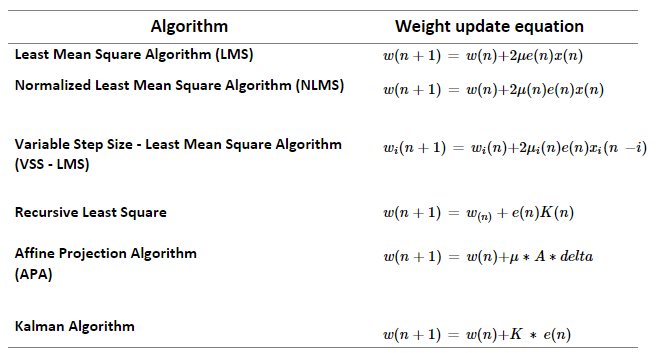
• Least Mean Square Algorithm (LMS) 
• Variable Least Mean Square Algorithm (VLMS) 
• Normalized Least Mean Square Algorithm (NLMS) 
• Recursive Least Square Algorithm (RLS) 
• Affine Projection Algorithm (APA) 
• Kalman Algorithm 

Among these algorithms, LMS, NLMS, VLMS, and RLS are generally considered as conventional adaptive filtering techniques.

The following outline the three basic steps for all algorithms:

1. Computing the output of the digital filter with a set of filter coefficients
2. Generation of an estimated error by comparing the filter output and desired signal
3. Adjusting filter coefficients based on the estimated error

Choosing the right kind of algorithm depends mainly on applications.

2.1.1 Least Mean Square Algorithm (LMS)

LMS Algorithm is a linear adaptive filtering algorithm and its a member of a stochastic gradient-based algorithm. An important feature of this algorithm is its robustness and low computational complexity. This is a fixed step-size algorithm and can be used in a wide range of applications such as channel equalization and echo cancellation, but it is not considered useful when a long echo duration is present as in case of teleconferencing. In teleconferencing, long impulse response or long memory is required to cope with the long duration of echo. LMS algorithm in time domain does not have a long memory to cope with the long-duration echo therefore it causes the problem of increased computational complexity. It mainly aims to reduce the mean square error between the signals. This algorithm uses a step size parameter to control immediate change in updating factor. As the value of step size decreases, the convergence speed to optimal values is slower and for large values, the filters will diverge and become unstable. So, we have to select the step size accordingly. It requires (2N+1) additions and (2N+1) multiplications, where N is length of adaptive filter.  

Filter coefficients updating equation in LMS,

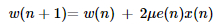
where,

• μ  – Step size, 0 < μ  < 1 
• x(n) – Input signal  
• e(n) – Error signal  

2.1.2 Normalized Least Mean Square Algorithm (NLMS)

By using the normalized step size parameter in LMS algorithm, it becomes NLMS algorithm. Normalized step size improves the convergence behavior in NLMS algorithm. So, it becomes more powerful in applications like speech recognition. This algorithm is an equally simple but more robust variant of LMS algorithm, and also keeps a better balance between simplicity and performance than LMS algorithm. In this algorithm, the step size parameter is chosen based on the current input values. As human speech has more energy in low frequencies, this algorithm gives good echo cancellation for low frequencies and poor for high frequencies. Step size varies adaptively by following the changes in input signal level which prevents filter weights from diverging and makes the algorithm more stable and faster converging compared with a fixed step size algorithm. NLMS algorithm requires (3N+1) multiplications and 1 division. 

Weight vector updating equation becomes, 

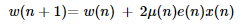
Step size for computing the weight updating factor is,

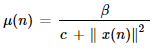
Where, 

• β – Normalized step size parameter, 0 <β<1 0 <?<1   
• c  – Safety factor is a positive constant, which prevents the division by a very small number of the data norm 

2.1.3 Variable Step Size – Least Mean Square Algorithm (VSS – LMS) 

VSS algorithm uses varying step size parameter. Large step size is used for faster convergence and small step size for reducing misalignment.  

At the beginning of adaptation process, filter weights are far from optimum values and step size should be large to converge rapidly but when it is approaching steady state solution, step size should decrease in order to reduce the mean square error.  

Filter coefficients can be updated using the following equation, 

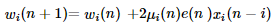
Where, 

• μi(n) –   Step size, a varying parameter 

VSS algorithm with normalization has (4N+1) multiplications and 1 division.  

2.1.4 Recursive Least Square  

In this method, the least squares estimate of filter weights is computed recursively in order to minimize the weighted least square cost function related to input signals. In LMS-based algorithms, MSE is minimized. Main advantages of RLS over other methods are its faster convergence, and minimum error at convergence but more complexity due to more complicated mathematical operations. It requires more computational resources than LMS algorithms. The instability of RLS algorithm makes it unsuitable for equalization purposes. RLS is more efficient to use on echo cancellation, channel equalization, and speech enhancement radar applications.  However, complexity of RLS algorithm prevents its usage. This algorithm requires (N²) Multiplications. 

Weight updating factor is updated using below equation, 

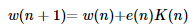
where,  

• K(n) – Gain vector 

2.1.5 Affine Projection Algorithm (APA) 

Affine projection LMS algorithm is also called as generalized NLMS algorithm. Compared to NLMS, APA not only considers errors at the current time but also takes hypothetical errors resulting from old data vectors filtered by the adaptive filter with current coefficient settings. It is a signal reuse algorithm and it has a good convergence rate compared to other traditional adaptive filtering algorithms. Step size parameter and projection length are the two important parameters that affect the performance of this algorithm. Increasing the projection order not only speeds up the convergence but also increases steady-state misalignment and computational complexity. If projection order M=1, then it behaves like NLMS algorithm. For speech applications projection order M=2 provides faster convergence. Suggested values of projection order (M) is between 2 to 5. The complexity of this algorithm is 2MN where N is length of adaptive filter.  

Weight updation equation is as follows, 

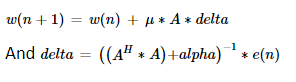
Where,  

• μ - Step size 
• A – Projection matrix 
• delta – Inverse of the normalization matrix 

2.1.6 Kalman Algorithm  

Kalman filters are computationally efficient, inherently robust, more accurate, and do not require any additional regularization or control mechanisms compared to other adaptive filtering techniques. This is also a recursive least squares error method for estimating distorted signals transmitted through channels or observed in noise. Kalman Filter is a prediction-correction model used in linear, time-variant, or time-invariant systems. Prediction model involves actual system and process noise. The updated model involves updating the predicated or estimated value with the observation noise. Kalman gain is calculated based on RLS algorithm in order to reach optimal value within less amount of time. Computational complexity of Kalman filter is N³.

Weight updating equation in Kalman algorithm is, 

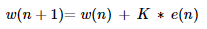
Where,  

• K - Kalman gain 

Weight update equation for different adaptive filters is shown in Table 1. 

3. Comparison 

The graphs below show the comparison of each algorithm in terms of its computational complexity and convergence rate. As per computational complexity, it is found that Kalman has more complexity than other algorithms.  

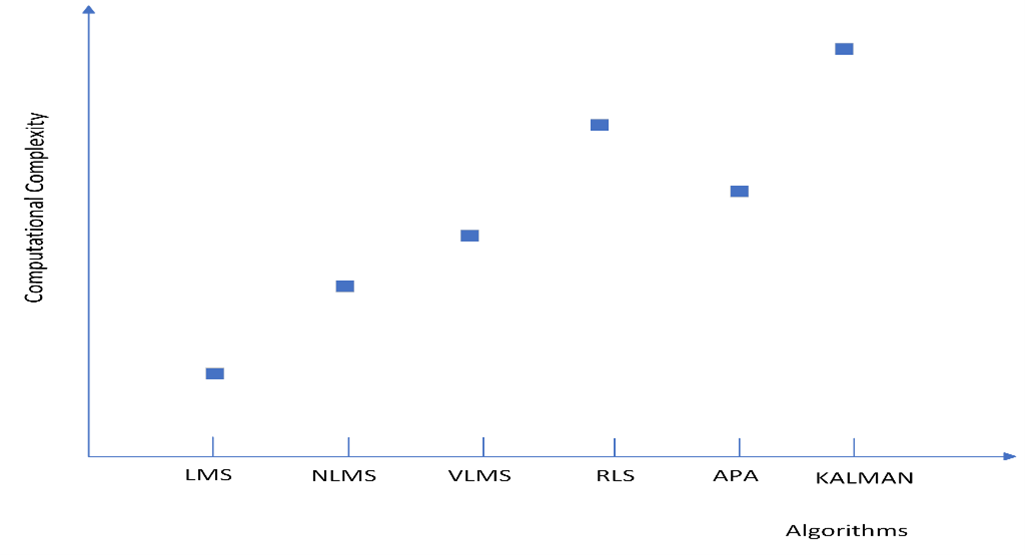
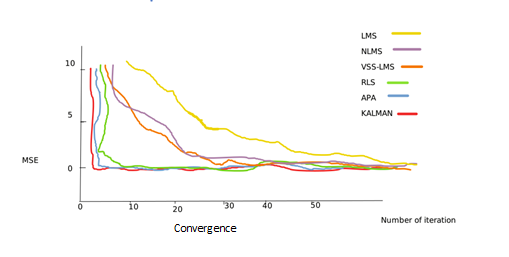
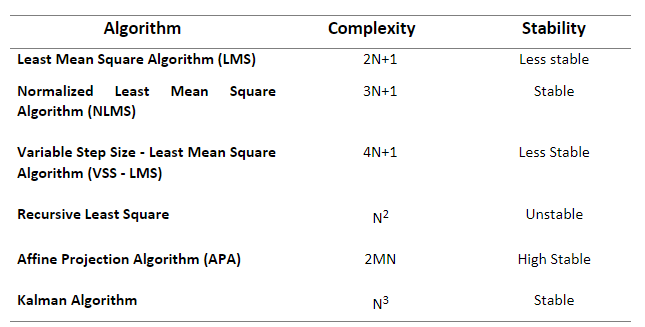
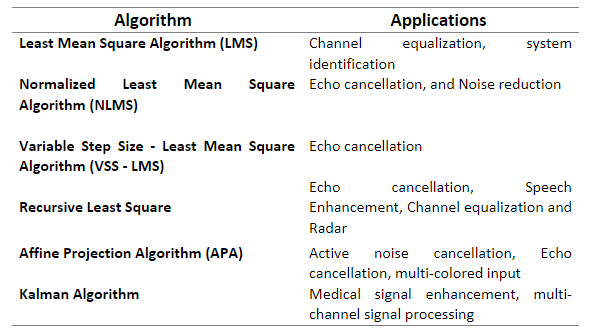
Choosing the right filter algorithm depends on many factors, including convergence performance, computational complexity, filter stability in the environment and applications. The table below shows the applications of different adaptive filters. 

4. Conclusion 

Performance of each algorithm varies depending on its applications, environment, and various other factors described before. LMS algorithms are best for channel equalization while RLS ones prove most efficient for echo cancellation. However, complexity of RLS algorithm prevents its usage, and thereby we can use NLMS/VSS-NLMS for echo cancellation depending upon the application priority. In the case of colored input applications, APA converges at a very fast rate when compared to other algorithms due to projection order. Kalman provides better results in signal enhancement applications. But it is more complex compared to all other algorithms. 

DSP is a focus area at Ignitarium and over the years, the team has been working on various audio algorithms, benchmarking, porting and optimization. A comparative study and implementation of time-domain and frequency-domain adaptive algorithms for acoustic echo cancellation were carried out. We implemented LMS, NLMS, APA, and Kalman adaptive filters for Echo cancellation, these are the most common applications of adaptive filtering. NLMS algorithm and Affine projection are more suitable for Echo cancellation, computational complexity of Kalman filters made them less attractive for the application. 

Ignitarium has developed a custom test framework to test these adaptive algorithms using different set of data sets that have control parameters and generate performance measures for each echo cancellation specific algorithm.