3D LiDAR SLAM – Scan Matching Explained  

Introduction to SLAM

Simultaneous Localization and Mapping (SLAM) is a popular technique in robotics that involves building a map of an unknown environment while simultaneously localizing the robot within that environment. This process is crucial for autonomous robots to navigate and operate effectively in complex, unstructured environments. 

SLAM algorithms typically use sensors such as cameras, LiDARs, and/or odometry sensors to gather data about the environment and the robot’s motion. The gathered data is then processed to estimate the robot’s position and orientation in the environment, as well as to build a map of the environment. 

The components of SLAM include the following: 

1. Sensor Data: LiDAR sensor data is used to measure distances to objects and generate 3D maps of the environment. 

2. Localization: The LiDAR SLAM algorithm estimates the robot’s pose (position and orientation) in real-time based on the LiDAR point cloud. 

3. Mapping: The point cloud generated from the LiDAR sensor is used to generate a map of the environment. (Read more about this subject in our blog on SLAM method used for Mapping based on data acquired from one or more sensors.)    

4. Scan Matching: The LiDAR SLAM algorithm uses scan matching to align consecutive LiDAR scans and estimate the robot’s pose. 

5. Feature Extraction: Salient features are identified from the LiDAR point cloud, which may include corners, line segments, or other geometric features. 

6. Feature Matching: The features from the current LiDAR scan are aligned with the features from the previous LiDAR scan to estimate the robot’s pose. 

You can further delve into the nuances of feature upgrades, which ensures more flexible, reliable, and safe robots that can perform a variety of tasks by collaborating with humans, ensuring reduced errors and enhanced safety in high-risk environments. To know more, read our blog on cobots and safety here.    

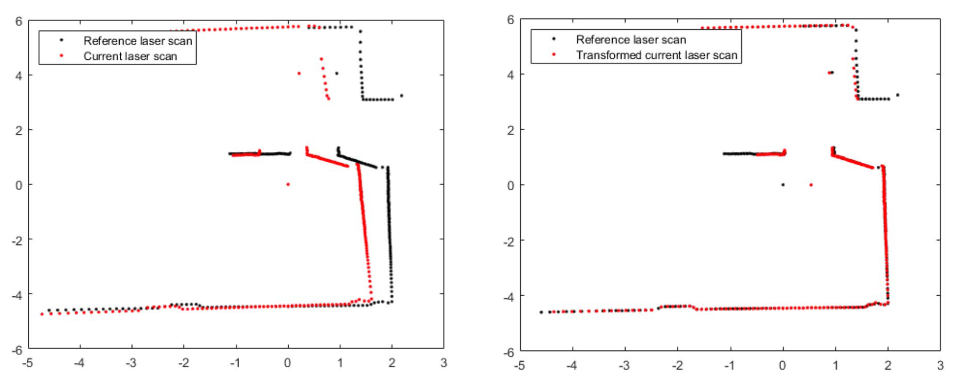
This blog discusses an important component of SLAM: Scan Matching, which involves aligning multiple scans (e.g., point clouds from a LiDAR) to estimate the robot’s pose. Scan matching is a critical step in SLAM because it allows the robot to determine its location within the environment. 

The LiDAR sensor sends out a laser beam, which reflects off the objects in the environment and returns to the sensor. The sensor measures the time it takes for the laser to return and calculates the distance to the object. By rotating the LiDAR sensor, multiple scans can be taken from different angles, generating a point cloud of the environment. The point cloud is then used to generate a map of the environment and estimate the robot’s pose. 

In the feature extraction stage, salient features are identified from the LiDAR point cloud. These features may include corners, line segments, or other geometric features that can be used to identify the environment’s structure. The features are then used to generate a map of the environment, which is then matched with the current LiDAR scan to estimate the robot’s pose. 

In the feature matching stage, the goal is to align the extracted features from the current LiDAR scan with the features from the previous LiDAR scan. 

What is Scan Matching? 

Scan matching is a crucial component of LiDAR SLAM, which estimates the motion pose of the current frame by analyzing the relationship between adjacent frames. It is commonly used in precise positioning and 6DOF state estimation of unmanned vehicles like aerial, ground, and aquatic.  

Iterative Closest Point (ICP) and Normal Distribution Transformation (NDT) are popular scan-matching algorithms that are used for local scan matching. ICP aligns two frames of point clouds based on distance judgment, while NDT uses a Gaussian distribution to model point clouds. 

Additionally, feature-based matching methods are also used, where features like line-plane features, viewpoint feature histograms, fast point feature histograms, 3D neighborhood point feature histograms, and density characteristics are utilized. The LOAM scheme is a well-known method that uses corner and plane point features for feature-based scan matching. 

This blog discusses in detail ICP and NDT algorithms and their variants.  

ICP 

The ICP algorithm is based on a model where there are two point clouds, a source point cloud P = {p1, p2, p3, …, pm} and a target point cloud Q = {q1, q2, q3, …, qn }, both of which are subsets of R3. The goal of the algorithm is to find a transformation matrix T that minimizes the error E(T) between P and Q. The error E(T) can be represented by the following equation: 

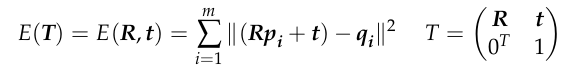
where R is the rotation matrix, t is the translation matrix, p is the point in the source point cloud, and q is the nearest point in the target point cloud. R, t can be solved by minimizing the above error function. 

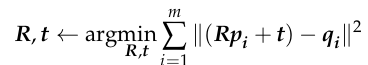
The algorithm can be written as: 

NDT 

The NDT algorithm involves two point clouds, a source point cloud P = {p1, p2, p3, …, pm} and a target point cloud Q = {q1, q2, q3, …, qn }, both of which are subsets of R3. In this algorithm, the target point cloud is divided into voxels, and the midpoints of each voxel are used to calculate the probability density function (PDF) for each voxel. The PDF is based on the distribution of points within the voxel and is used to obtain the position of a point on the target point cloud through random processing of the D-dimensional normal distribution. 

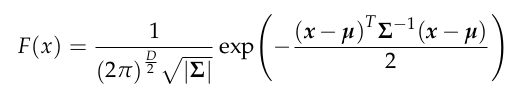
where D represents the dimension, µ and Σ represent the mean vector and covariance matrix of all points in the voxel where x is located, respectively, µ and Σ are calculated by the following formulas 

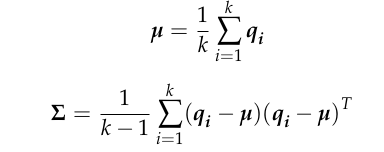
q_i = 1,,,,k is the position coordinates of all points contained in the voxel. 

After the probability density function (PDF) is calculated for each voxel in the target point cloud, the NDT algorithm obtains the pose transformation T that maximizes the overall likelihood of the transformed source point cloud in its corresponding PDF. The transformed source point cloud is obtained by applying the pose transformation T to the source point cloud P. The goal of this step is to align the transformed source point cloud with the target point cloud by maximizing their overall likelihoods. 

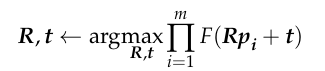
Comparing ICP and NDT 

1. Efficiency: ICP is generally faster than NDT because it involves finding the nearest neighbors of points in the two-point clouds, which can be done efficiently using spatial data structures. In contrast, NDT involves voxelization and PDF calculation, which can be computationally expensive. 

2. Robustness: NDT is more robust to noise and outliers in the point clouds because it models the distribution of points within each voxel using a PDF. This helps to reduce the effect of noise and outliers on the alignment process. ICP, on the other hand, is more sensitive to noise and outliers because it relies on finding the nearest neighbors of points in the two point clouds. 

3. Accuracy: NDT can provide higher accuracy than ICP because it models the distribution of points within each voxel and can therefore capture the shape of the target object more accurately. ICP, on the other hand, relies on finding the closest point in the target cloud for each point in the source cloud, which may not always capture the full shape of the target object. 

4. Applicability: ICP is more widely applicable than NDT because it can be used with any point cloud, regardless of the density and distribution of points. NDT, however, requires the target point cloud to be voxelated, which can limit its applicability in some scenarios. 

ICP Variants 

The Iterative Closest Point (ICP) algorithm is widely used for point cloud registration in robotics and computer vision. However, it has several shortcomings, including sensitivity to the initial value, high computational overhead, easily being trapped in a local optimal solution, and a lack of utilization of point cloud structure information. To address these issues, experts and scholars have proposed various improved ICP algorithms. 

One such improvement is the Point-to-Line ICP (PLICP) algorithm that replaces the point-to-point distance metric with point-line distance metric.This approach improves accuracy and requires fewer iterations but is more sensitive to initial values. Another improvement is the Point-to-Plane ICP (P2PL-ICP) algorithm, which uses the distance from the point to the surface instead of the distance from the point to the point to improve the convergence speed. 

The Generalized-ICP (GICP) algorithm combines P2P-ICP and P2PL-ICP into a probabilistic framework based on which point cloud matching is carried out. The covariance matrix eliminates some bad corresponding points in the solution process. GICP algorithm can effectively reduce the impact of mismatches and is one of the most effective and robust algorithms among many improved ICP algorithms. 

Other improvements include ICP using invariant features (ICPIF), Multi-scale ICP (MbICP), Normal-distributions transform (NDT), Continuous-ICP (CICP), Enhanced ICP, AA-ICP (using Anderson acceleration), and Robust ICP with Sparsity Induction Norms. 

NDT Variants 

The Normal Distribution Transform (NDT) algorithm was initially developed by Biber and Strasser for 2D scan matching, which was later extended to 3D by Magnusson et al. A comparison between NDT and ICP algorithms for 3D scan matching showed that NDT is faster and converges from a wider range of initial pose estimations, but its convergent pose is unpredictable and can generate worse results than ICP in case of failure. Several modifications and extensions have been proposed to improve the efficiency, accuracy, and robustness of NDT registration, including trilinear interpolation, multi-threading, semantic labeling, variable voxel size, multi-layer-based transformation, feature extraction, and probability-based point sampling. Some of these methods have shown better performance and higher accuracy than the classical NDT algorithm in specific applications. For example, the weighted NDT method uses the static probability of each point as a weight to improve classification accuracy, while the SEO-NDT algorithm and its FPGA implementation achieve faster processing of larger point clouds in real-time. The FGO-NDT algorithm uses factor graph optimization to eliminate pose drift error and improve local structure in large scenes. 

Conclusion 

In conclusion, ICP and NDT are two widely used scan-matching algorithms for point cloud registration in the field of robotics, autonomous driving, and computer vision. While ICP is a simple and fast algorithm, it has limitations when dealing with large point clouds, noisy data, and outliers. On the other hand, NDT, which is based on the normal distribution transform, has shown itself to be more robust and accurate in these challenging scenarios. NDT also performs better than ICP in terms of convergence rate and the ability to handle a wider range of initial pose estimations. 

However, NDT has some drawbacks such as unpredictable convergence poses and longer computation time. To address these issues, various modifications and improvements have been proposed, including trilinear interpolation, semantic labels, variable voxel size, multi-layer-based transformation, and factor graph optimization. These modifications have significantly enhanced the efficiency and robustness of the NDT algorithm and made it suitable for real-time applications. 

In summary, both ICP and NDT have their advantages and limitations, and the choice of the algorithm depends on the specific requirements of the application. 

Ignitarium’s Robotics and Perception AI Software team brings expertise on enabling the software stack for Autonomous Navigation, SLAM, Localization, Path Planning and Perception, making reliable implementations a reality, hence driving up ROI for adopters in the long run.